Researchers from the University of Copenhagen have included parameters that consider a spatially heterogeneous population for transmission in a new model for airborne disease transmission. This allows for estimating superspreaders and appropriate mitigation strategies.
The rapid spread of COVID-19 has lead to many efforts to model and predict how the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) spreads. Key questions when trying to model disease spread are how easily it is transmitted and how long affected individuals are affected.
One method to estimate disease spread is to use the basic reproduction number (R0). In epidemiology, the basic reproduction number of an infection can be thought of as the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection. The definition describes the state where no other individuals are infected or immunized (naturally or through vaccination). However, this number can be misleading because not all infected people actually transmit the infection to others. Instead, disease spread occurs because a few people who infect a lot of others.
There could be many reasons for this. For example, there may be something inherent biologically that makes some people spread infection more, or makes them superspreaders. This is something that has been seen during the COVID-19 pandemic.
Another reason could be how people interact with others may be different, or social interactions are heterogeneous. Models like Susceptible-Infected-Recovered (SIR) take these variations into account but assume that an individual interacts with only one other person at a time.
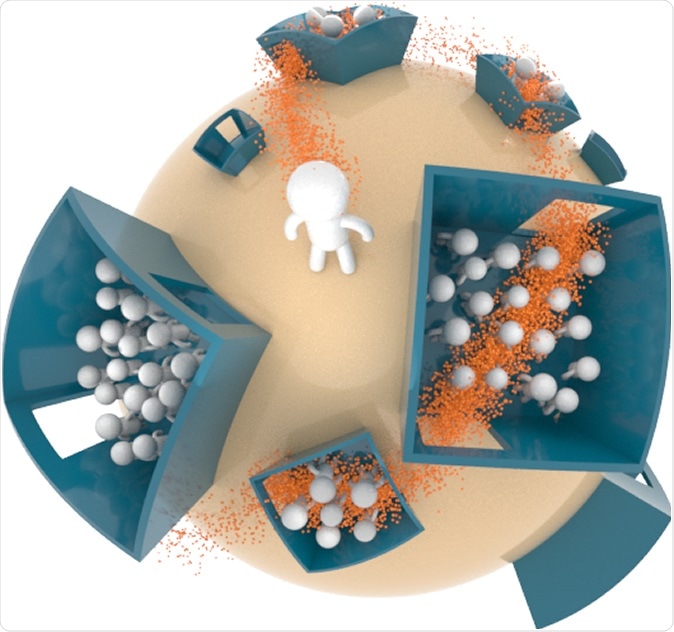
Model includes a heterogeneous population
In a new medRxiv* preprint paper, researchers propose a new model for disease spread, for example, SARS-CoV-2-like airborne infections, where one person can infect many. In their model world, people move from one place to another and infect all people within some distance of the infected person. How long a person is infectious is captured by a parameter M, with M increasing if the disease has a long infectiousness period.
In their social world model, they use visits to different locations with different numbers of people gathered.
For example, if people are exponentially distributed in various locations, for a certain R0, the number of secondary infections will be a negative binomial distribution. For R0 more than or equal to 1, 20% of the most infectious persons will infect up to 65% of people.
However, since real-life gatherings are usually much larger, the authors used a probability density function with a fat tail. The model includes instances where infected people go to rare events, and a single person can infect many at the same time. The model can be used both for a population of a country as well as a small neighborhood.
Upon solving the model analytically, the authors found that a disease that has a short period of infectiousness will be more prone to superspreading. If people are aware they are infectious, they will isolate themselves and prevent spread. Thus, diseases, where people are asymptomatic with a short period of infectivity, may be driven by superspreading events.
The authors also captured how mitigation strategies affect spread by calculating how these efforts affect R0. They found if small gatherings are banned, the R0 increases, as the people who would have gone to those now go to larger gatherings.
But, if locations with medium to large size gatherings are closed R0 decreases. Although it would be intuitive to close all places with large gatherings and work for diseases with any length of infectivity, the authors write that it is important to look at gathering habits in a community before choosing the size of gatherings to be banned.
Estimating superspreaders
Based on their analysis, the authors say 20% of infected people may infect 80% even if there are no biological superspreaders. Thus, in any epidemic, to determine if superspreaders are important in disease transmission, it should be compared to a model that includes spatial heterogeneity and infectiousness duration rather than a simple model that assumes a homogeneous population.
Although the model works even when the probability of a person being at a particular location is not known, the results improve if that parameter is known, as they demonstrated using location data for about 650 students.
The authors write that their model could also be used to include biological superspreaders. This can be done, for example, using a dispersed probability distribution for infectivity rather than using a constant value.
It is known that SARS-CoV-2 is an airborne pathogen, and viral loads and infectiousness peaks for short durations of a day or two. It has also been suggested that superspreaders are a big factor in driving the COVID-19 pandemic.
“It is thus of paramount importance to fully understand the true distribution of superspreaders, taking into account that superspreading statistics can result from many sources, one being socio-spatial heterogeneity,” write the authors.
*Important Notice
medRxiv publishes preliminary scientific reports that are not peer-reviewed and, therefore, should not be regarded as conclusive, guide clinical practice/health-related behavior, or treated as established information.
https://news.google.com/__i/rss/rd/articles/CBMid2h0dHBzOi8vd3d3Lm5ld3MtbWVkaWNhbC5uZXQvbmV3cy8yMDIwMTAyOS9Nb2RlbC1pbmNsdWRlcy1zcGF0aWFsLWhldGVyb2dlbmVpdHktdG8tYW5hbHl6ZS1haXJib3JuZS1kaXNlYXNlLXNwcmVhZC5hc3B40gF7aHR0cHM6Ly93d3cubmV3cy1tZWRpY2FsLm5ldC9hbXAvbmV3cy8yMDIwMTAyOS9Nb2RlbC1pbmNsdWRlcy1zcGF0aWFsLWhldGVyb2dlbmVpdHktdG8tYW5hbHl6ZS1haXJib3JuZS1kaXNlYXNlLXNwcmVhZC5hc3B4?oc=5
2020-10-30 02:32:00Z
52781155734675
Bagikan Berita Ini














0 Response to "Model includes spatial heterogeneity to analyze airborne disease spread - News-Medical.Net"
Post a Comment